2to1 変則 3 本組みスポーク長計算2014-08
こないだ組んだ 32h を 24 本で組む変則 2to1 リアホイールの半分に間引く反フリー側である 3 本組みのスポーク長を真面目に計算してみようと思うよ。 プログラマー時代はウンウン唸りながらこんな計算やってたけど、久しぶりの今はちょっと楽しい!
基本はこのパターン
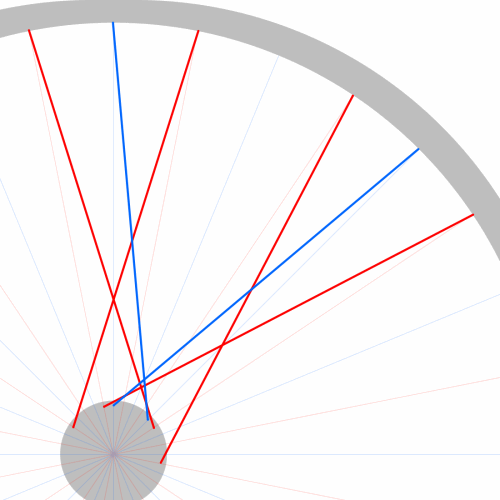
赤がフリー側の普通の 6 本組み。 そして青が反フリー側の珍しい 3 本組みで、リム側の穴飛ばし数もフリー側 1 つ飛ばしに対して反フリー側は 3 つ飛ばしという超変則。 まずはこの 2 次元平面図で計算をしてみようか。
中心点はハブの中心と定める
いわゆる [ X座標:0, Y座標:0 ] のポイントをハブの中心として計算します。
まずはハブ穴座標を算出
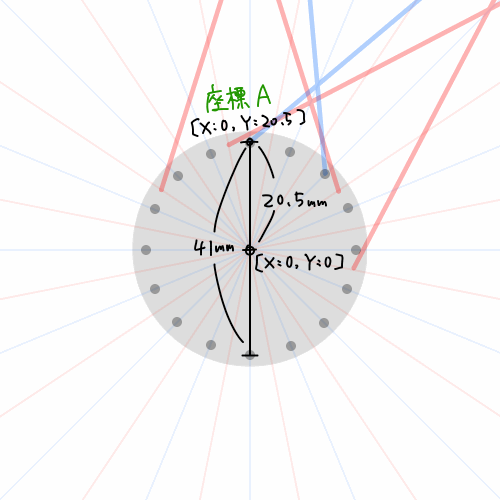
ハブの反フリー側の PCD を今度使おうと思っている TNI エボリューションライトと同じく 41mm と仮定すると、ハブ穴座標は [X:0, Y:20.5] になりもす! そしてこれを [座標A] としもす。
続いてリム穴座標を算出
手持ちの SUNRINGLE UFO のリムの内径を測ったら 530mm だったので、半径は 265mm となりもす。 そしてさっき測った [座標A] に通したスポークが入るリム穴とハブ中心点を結んだ線の傾き角度は 45°。 これを図にすると以下の様な感じですね↓
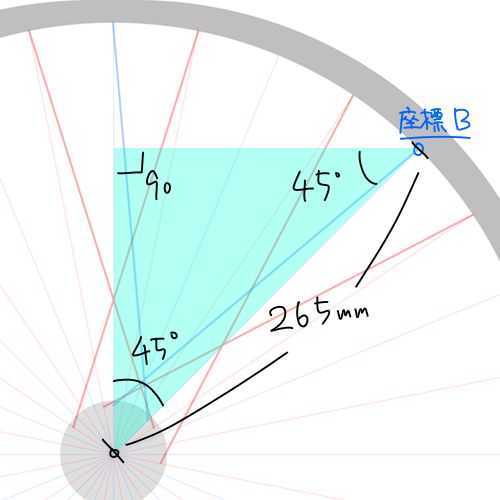
さあここから [座標B] の X 座標と Y 座標を求めると、いやこれは 2 等辺三角形だから長さが同じなので X 座標だけを求めると
| X | = | 265 x sin(45); |
| = | 265 x 0.707106781186548; | |
| = | 187.383297014435088; |
そして[座標A] と [座標B] の距離を算出
今までの計算を元にしたこんな感じ↓の三角形の [辺C] を求めるだけ。
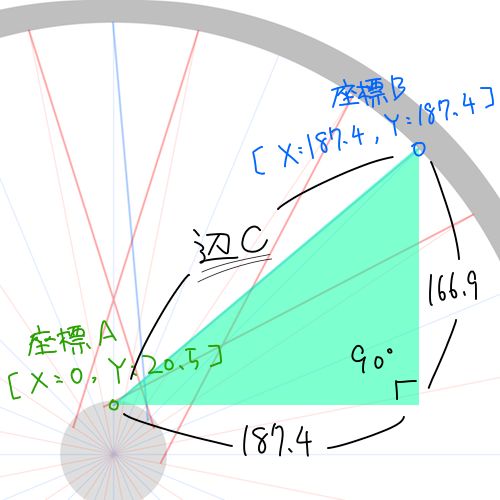
てことは計算はこうね。
| [辺C]² | = | 187.4² + 166.9²; |
| = | 35112.499999999997577 + 27850.034822408158989; | |
| = | 62962.534822408156566; | |
| [辺C] | = | √62962.534822408156566; |
| = | 250.9233644410344; |
最後に奥行きを加味して終了!
今までのホイールの向きを正面からとすると、今度は横から見ます。 TNI エボリューションライトの反フリー側のセンターフランジ間距離 36.93mm を書き加えて図にしたのがこれね↓
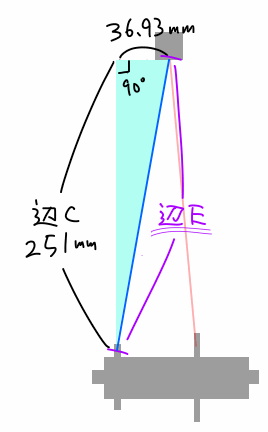
さあさあこれで最後の [辺E] を計算すると
| [辺E]² | = | 250.9233644410344² + 36.93²; |
| = | 62962.53482240816677 + 1363.8249; | |
| = | 64326.35972240816677; | |
| [辺E] | = | √64326.35972240816677; |
| = | 253.6264176350882 |
何と!
TNI レボリューションライトのハイローフランジのおかげか、今回算出した反フリー側のスポーク長 258mm はフリー側と全く同じ。 もしかしてどっちも同じ長さでイケるんちゃう? だとしたら素晴らしいかも!
とはいうものの
スポークはおろかまだハブも手に入れていないのでこれは取らぬ狸の皮算用というやつ。 散財の覚悟ができたらハブ買うぞ!
ハブ買った!
これ書いた後けっこうすぐ投資で儲かったのでハブ購入。 本組みはコチラ! 256mm くらいが丁度良さそう!